TIPOS DE FUNCIONES

Tipos de funciones

Dependiendo de ciertas características que tome la expresión algebraica o notación de la función f en x, tendremos distintos tipos de funciones:

Función constante

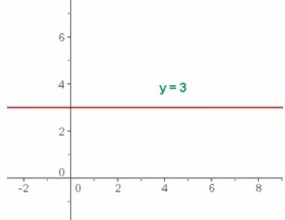
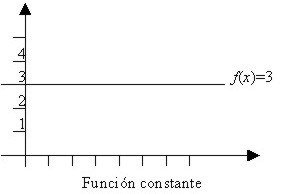
Una función de la forma f(x) = b, donde b es una constante, se conoce como una función constante.

Por ejemplo, f(x) = 3, (que corresponde al valor de y) donde el dominio es el conjunto de los números reales y el recorrido es {3}, por tanto y = 3. La gráfica de abajo muestra que es una recta horizontal.

Función lineal

Una función de la forma f(x) = mx + b se conoce como una función lineal, donde m representa la pendiente y b representa el intercepto en y. La representación gráfica de una función lineal es una recta. Las funciones lineales son funciones polinómicas.

Ejemplo:

f(x) = 2x − 1  

es una función lineal con pendiente m = 2 e intercepto en y en (0, −1). Su gráfica es una recta ascendente.

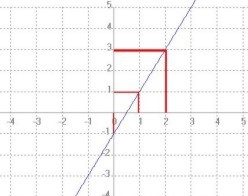f(x) = 2x − 1

En general, una función lineal es de la forma 

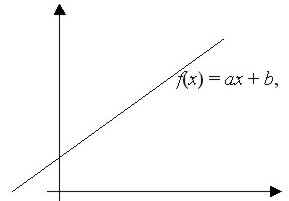f(x) = ax + b, donde a y b son constantes (la a es lo mismo que la m anterior (corresponde a la pendiente).

Función cuadrática

Una función de la forma f(x) = ax² + bx + c, donde a, b y c son constantes y a es diferente de cero, se conoce como una función cuadrática.

La representación gráfica de una función cuadrática es una parábola. Una parábola abre hacia arriba si a > 0 y abre hacia abajo si a < 0.  El vértice de una parábola se determina por la fórmula:

Las funciones cuadráticas son funciones polinómicas.

Ejemplo:

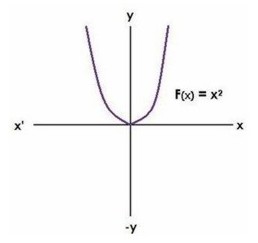f(x) = x2  representa una parábola que abre hacia arriba con vértice en (0,0).

Función racional

Una función racional es el cociente de dos funciones polinómicas. Así es que q es una función racional si para todo x en el dominio, se tiene:

para los polinomios f(x) y g(x).

Ejemplos:

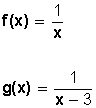
Nota: El dominio de una función polinómica son los números reales; sin embargo, el dominio de una función racional consiste de todos los números reales excepto los ceros del polinomio en el denominador (ya que la división por cero no está definida).

Función  de potencia

Una función de potencia es toda función de la forma  f(x) = x^r, donde r es cualquier número real.

Las funciones f(x) = x^4/3 y  h(x) = 5x^3/2 son funciones de potencia