FUNCION MONOTONA

Definicion: Funcion Monotona

En matemáticas, una función entre conjuntos ordenados se dice monótona (o isótona) si conserva el orden dado. Las funciones de tal clase surgieron primeramente en cálculo, y fueron luego generalizadas al entorno más abstracto de la teoría del orden. Aunque los conceptos generalmente coinciden, las dos disciplinas han desarrollado una terminología ligeramente diferente; mientras en cálculo se habla de funciones monótonamente crecientes y monótonamente decrecientes (o simplemente crecientes y decrecientes), en la teoría del orden se usan los términos monótona y antítona, o se habla de funciones que conservan e invierten el orden.

EJEMPLO GRAFICO.

A continuación se muestran tres gráficas de funciones cualesquiera. La primera de ellas es una función estrictamente creciente por la izquierda y por la derecha, mientras que es constante en el medio; por lo demás, es creciente pues conserva el orden ascendente durante todo el recorrido de la función. La segunda de ellas es escrictamente decreciente por la izquierda y por la derecha, puesto que conserva el orden descendente durante todo el recorrido de la función. La última de ellas es una función con un recorrido con partes donde la función es creciente y partes donde es decreciente (presenta máximos y mínimos relativos).

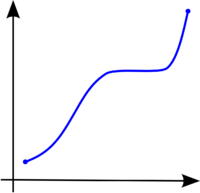Función monótona creciente.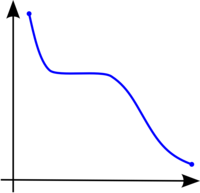

Función monótona decreciente.

Función no monótona.