FUNCIONES PARES E IMPARES

Definicion: Funciones Par E Impar

Una función es par si cumple que:

f(-x) = f(x)

Una función es simétrica respecto del eje de ordenadas si ésta es una función par.

Una función es impar si cumple que:

f(-x) = -f(x)

Una función es simétrica respecto al origen si ésta es una función impar.

Se dice que una función es par si f(x) = f(-x), en el caso de que f(x) = -f(-x) se dice que la función es impar.

Ejemplos 1:
La función y(x)=x  es impar ya que:
 f(-x) = -x                                                           
 pero como f(x) = x entonces:
f(-x) = - f(x).

Ejemplo 2:
Otra función impar es y = 1/x
Cuando f(x) = -f(-x)
                      

Ejemplo 3:
La función f(x)=x² es par  ya que f(-x) = (-x)² =x²

FUNCION MONOTONA

Definicion: Funcion Monotona

En matemáticas, una función entre conjuntos ordenados se dice monótona (o isótona) si conserva el orden dado. Las funciones de tal clase surgieron primeramente en cálculo, y fueron luego generalizadas al entorno más abstracto de la teoría del orden. Aunque los conceptos generalmente coinciden, las dos disciplinas han desarrollado una terminología ligeramente diferente; mientras en cálculo se habla de funciones monótonamente crecientes y monótonamente decrecientes (o simplemente crecientes y decrecientes), en la teoría del orden se usan los términos monótona y antítona, o se habla de funciones que conservan e invierten el orden.

EJEMPLO GRAFICO.

A continuación se muestran tres gráficas de funciones cualesquiera. La primera de ellas es una función estrictamente creciente por la izquierda y por la derecha, mientras que es constante en el medio; por lo demás, es creciente pues conserva el orden ascendente durante todo el recorrido de la función. La segunda de ellas es escrictamente decreciente por la izquierda y por la derecha, puesto que conserva el orden descendente durante todo el recorrido de la función. La última de ellas es una función con un recorrido con partes donde la función es creciente y partes donde es decreciente (presenta máximos y mínimos relativos).

Función monótona creciente.

Función monótona decreciente.

Función no monótona.

FUNCIONES CRECIENTES & DECRECIENTES

Defincion: Funcion Creciente & Decreciente

Una función f es creciente es un intervalo si para cualquier par de números x₁,x₂ del intervalo..

Una fución f es decreciente es un intervalo si para cualquier par de números x₁,x₂ del intervalo, .

Sea f una función continua con ecuación y = f(x), definida en un intervalo [a,b]. La siguiente es la representación gráfica de f en el intervalo[a,b]. 

En la gráfica anterior puede observarse que la función f es:

1.) Creciente en los intervalos (a,x3),(x5,x6)

2.) Decreciente en los intervalos(x3,x5),(x6,b)

Definicion: Funcion Inversa

Sabemos que una función es un conjunto de pares. Se nos puede ocurrir la idea de dar la vuelta a los pares y obtener así una nueva función. Hagámoslo con la función:

f = { (1, 2), (2, 4), (3, -1), (4, -2) }

y observemos qué pasa llamando g al conjunto resultante:

g = { (2, 1), (4, 2), (-1, 3), (-2, 4) }

Hemos obtenido una nueva función.

Sin embargo, esto no funciona siempre. Tomemos ahora como f el conjunto:

f = { (1, 2), (2, 4), (3, -1), (4, 2) }

y, entonces, g será:

g = { (2, 1), (4, 2), (-1, 3), (2, 4) }

que no es una función, pues g(2) no está determinado de forma única; es decir, g no cumple la condición de función. Existen dos pares, (2, 1) y (2, 4), que tienen la misma primera coordenada y la segunda coordenada es distinta.

¿Cuál es la diferencia entre estos dos ejemplos? Sencillamente, que en el segundo ejemplo f(1)=f(4)=2 y al darle la vuelta a los pares, g(2) no está determinado de forma única; con lo cual g no es una función. En el primer ejemplo, para valores diferentes de la "x" se obtienen valores diferentes de la "y". Las funciones que se comportan como la del primer ejemplo se llaman funciones inyectivas o uno a uno.

DEFINICIÓN: Una función f es inyectiva o uno a uno si f(a) es distinto de f(b) cuando a es distinto de b.

Cuando al invertir los pares de que consta una función se obtiene otra función, decimos que dicha función tiene inversa (también llamada recíproca). Por lo dicho anteriormente, sólo tienen inversas las funciones inyectivas.

DEFINICIÓN: Si f es una función inyectiva, llamamos función inversa de f y la representamos por f-1 al conjunto:

f-1 = { (a, b) / (b, a) Î f }

Es decir, f-1 = { (x, y) / x=f(y), si y es del dominio de f } = { (f(y), y) / si y es del dominio de f }

De la definición se sigue inmediatamente que el dominio de la función inversa f-1 es el rango de f y, recíprocamente, el rango de f-1 es el dominio de f. También es fácil observar que f-1(a)=b es equivalente a decir que f(b)=a. Utilizando la "x" y la "y" que tan acostumbrado estamos a usarlas cuando se habla de funciones: f-1(x)=y es equivalente a decir que f(y)=x. Otra forma de decir esto es: f(f-1(x))=x (donde x pertenece al rango de f), o bien, f-1(f(x))=x (donde x pertenece al dominio de f). Utilizando la composición de funciones y llamando I (función Identidad) a la función definida por I(x)=x, podemos escribir:

fof-1 = I y f-1of = I

salvo que el segundo miembro de estas dos igualdades tendrá un dominio más amplio que el primer miembro si el dominio de f o de f-1 no es todo R.

Por cierto, si una función tiene inversa, ¿a qué será igual (f-1)-1, o sea, la función inversa de la función inversa?

La idea de función inversa se ha utilizado muchas veces en los cursos anteriores a este nivel, sólo que no se le ha dado nombre. Recordar cómo se definía raíz cuadrada, cúbica...

Para determinar si una función tiene inversa tenemos que observar sus pares y ver si es inyectiva. Esto es muy fácil de hacer cuando la función viene dada por una lista de pares. Cuando la función viene definida por una propiedad, todo se complica y no siempre tendremos suficientes conocimientos matemáticos para determinar tal circunstancia (del mismo modo que nos pasaba cuando queríamos determinar si un determinado conjunto era o no función).

La representación gráfica de la función nos permitirá saber si la función tiene inversa o no, al menos en los casos más comunes. Basta observar que la definición de función inyectiva significa, gráficamente, que no hay dos puntos de la función situados sobre la misma recta horizontal. O dicho de otra forma, a partir de la representación gráfica de f, se construye la representación gráfica del conjunto de pares invertidos y se observa si este conjunto es función o no.

EJEMPLOS:

La función f definida por y=2x-3, es decir, f = { (x, y) / y=2x-3 } = { (x, 2x-3) } tiene inversa y su inversa será f-1 = { (y, x) / y=2x-3 } = { (x, y) / x=2y-3 } = { (2x-3, x) }

La función g definida por y=x2-2x-2, es decir, g = { (x, y) / y=x2-2x-2 } = { (x, x2-2x-2) } no tiene inversa. Por ejemplo, los pares (0, -2) y (2, -2) pertenecen a g y por lo tanto, g no es inyectiva.

La siguiente escena presenta ambos ejemplos. La función f o g aparecerá en azul y el conjunto de pares invertidos en rosa. Un control que se mueve a través de las funciones nos va mostrando un par de la función y otro punto nos presenta el correspondiente par invertido. Se podrá observar también en la escena una recta, la bisectriz del primer y tercer cuadrante (la recta de ecuación y=x). Observar que las gráficas de una función y de su conjunto de pares invertidos son simétricas respecto de dicha recta.

FUNCIONES TRASCENDENTES

Deifinicion: Funciones Transcendentes

Las funciones racionales y las irracionales, que han sido tratadas en las páginas anteriores, se denominan funciones algebraicas.
Las  funciones que no son algebraicas se llaman funcionestrascendentes.
Son funciones trascendentales elementales 

• Función exponencial: 

f(x)=a^x; a > 0, a ≠ 1.

• Función logarítmica:f(x)=log_a(x); a > 0, a ≠ 1. Es inversa de la exponencial.
  
• Funciones trigonométricas:También llamadas circulares
  
  f(x)=sen(x); f(x)=cos(x); f(x)=tg(x); f(x)=cosec(x); f(x)=sec(x) y f(x)=cotg(x)
  
  

Una función trascendente es una función que no satisface una ecuación polinómica cuyos coeficientes sean a su vez polinomios; esto contrasta con las funciones algebraicas, las cuales satisfacen dicha ecuación. En otras palabras, una función trascendente es una función que trasciende al álgebra en el sentido que no puede ser expresada en términos de una secuencia finita de operaciones algebraicas de suma, resta y extracción de raíces. Una función de una variable es trascendente si es independiente en un sentido algebraico de dicha variable.

FUNCIONES INYECTIVA, SOBREYECTIVA Y BIYECTIVA.

Definicion: Inyectiva

Una función f es inyectiva si, cuando f(x) = f(y), x = y.

Ejemplo: f(x) = x² del conjunto de los números naturales  a  es una función inyectiva.

(Pero f(x) = x² no es inyectiva cuando es desde el conjunto de enteros  (esto incluye números negativos) porque tienes por ejemplo

·         f(2) = 4 y

·         f(-2) = 4)

Nota: inyectiva también se llama "uno a uno", pero esto se confunde porque suena un poco como si fuera biyectiva.

Definicion: Sobreyectivo (o también "epiyectivo")

Una función f (de un conjunto A a otro B) es sobreyectiva si para cada y en B, existe por lo menos un x en Aque cumple f(x) = y, en otras palabras f es sobreyectiva si y sólo si f(A) = B.

Así que cada elemento de la imagen corresponde con un elemento del dominio por lo menos.

Ejemplo: la función f(x) = 2x del conjunto de los números naturales  al de los números pares no negativos es sobreyectiva.

Sin embargo, f(x) = 2x del conjunto de los números naturales  a  no es sobreyectiva, porque, por ejemplo, ningún elemento de  va al 3 por esta función.

Definicion: Biyectiva

Una función f (del conjunto A al B) es biyectiva si, para cada y en B, hay exactamente un x en A que cumple que f(x) = y

Alternativamente, f es biyectiva si es a la vez inyectiva y sobreyectiva.

Ejemplo: La función f(x) = x² del conjunto de números reales positivos al mismo conjunto es inyectiva y sobreyectiva. Por lo tanto es biyectiva.

(Pero no desde el conjunto de todos los números reales porque podrías tener por ejemplo

·         f(2)=4 y

·         f(-2)=4)

TIPOS DE FUNCIONES

Tipos de funciones

Dependiendo de ciertas características que tome la expresión algebraica o notación de la función f en x, tendremos distintos tipos de funciones:

Función constante

Una función de la forma f(x) = b, donde b es una constante, se conoce como una función constante.

Por ejemplo, f(x) = 3, (que corresponde al valor de y) donde el dominio es el conjunto de los números reales y el recorrido es {3}, por tanto y = 3. La gráfica de abajo muestra que es una recta horizontal.

Función lineal

Una función de la forma f(x) = mx + b se conoce como una función lineal, donde m representa la pendiente y b representa el intercepto en y. La representación gráfica de una función lineal es una recta. Las funciones lineales son funciones polinómicas.

Ejemplo:

f(x) = 2x − 1  

es una función lineal con pendiente m = 2 e intercepto en y en (0, −1). Su gráfica es una recta ascendente.

f(x) = 2x − 1

En general, una función lineal es de la forma 

f(x) = ax + b, donde a y b son constantes (la a es lo mismo que la m anterior (corresponde a la pendiente).

Función cuadrática

Una función de la forma f(x) = ax² + bx + c, donde a, b y c son constantes y a es diferente de cero, se conoce como una función cuadrática.

La representación gráfica de una función cuadrática es una parábola. Una parábola abre hacia arriba si a > 0 y abre hacia abajo si a < 0.  El vértice de una parábola se determina por la fórmula:

Las funciones cuadráticas son funciones polinómicas.

Ejemplo:

f(x) = x2  representa una parábola que abre hacia arriba con vértice en (0,0).

Función racional

Una función racional es el cociente de dos funciones polinómicas. Así es que q es una función racional si para todo x en el dominio, se tiene:

para los polinomios f(x) y g(x).

Ejemplos:

Nota: El dominio de una función polinómica son los números reales; sin embargo, el dominio de una función racional consiste de todos los números reales excepto los ceros del polinomio en el denominador (ya que la división por cero no está definida).

Función  de potencia

Una función de potencia es toda función de la forma  f(x) = x^r, donde r es cualquier número real.

Las funciones f(x) = x^4/3 y  h(x) = 5x^3/2 son funciones de potencia

DEFINICIONES: FUNCION, DOMINIO, COTRADOMINO & RANGO

Definicion: Funcion

Existen diferentes tipos de expresiones algebraicas, sin embargo algunas de las expresiones que mas nos interesa dentro del cálculo son las funciones.Una función es una regla de asociación que relaciona dos o mas conjuntos entre si; generalmente cuando tenemos la asociación dos conjuntos las función se define como una regla de asociación entre un conjunto llamado dominio con uno llamado codominio, también dominio e imagen respectivamente o dominio y rango. Esta regla de asociación no permite relacionar un mismo elemento del dominio con dos elementos del codominio.

Defincion: Dominio

En matemáticas, el dominio (conjunto de definición o conjunto de partida) de una función  es el conjunto de existencia de ella misma, es decir, los valores para los cuales la función está definida. Es el conjunto de todos los objetosque puede transformar, se denota   o bien  . En  se denomina dominio a un conjunto conexo, abierto y cuyo interior no sea vacío. Por otra parte, el conjunto de todos los resultados posibles de una función dada se denomina imagen de esa función.

Definicion: Contradominio

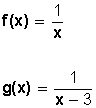
En matemáticas, el codominio o contradominio (también denominado conjunto final, recorrido o conjunto de llegada) de una función  es el conjunto que participa en esa función, y se denota  o  o .

Sea  la imagen de una función , entonces .

Definicion: Rango

El rango de una función, está determinado por todos los valores que pueden resultar al evaluar una función. Son los valores obtenidos para la variable dependiente (y). También se puede expresar como todos los valores de salida de la función.

Por ejemplo:

Si x=2, evaluamos f(2) = 2 ^2 = 4. Y así podemos hacerlo con cualquier número, positivo o negativo. Como x está elevada al cuadrado todos los valores resultantes (es decir de salida) son positivos. Con lo anterior se obtiene que elrango está conformado por el cero y todos los números positivos.

Al graficar la función se obtiene:

Para obtener el rango desde el punto de vista gráfico, debemos poner nuestra atención en el eje y. Se puede ver que el rango está dado por valores mayores o iguales que cero, pues la parábola que lo representa esta ubicada del eje x hacia arriba.